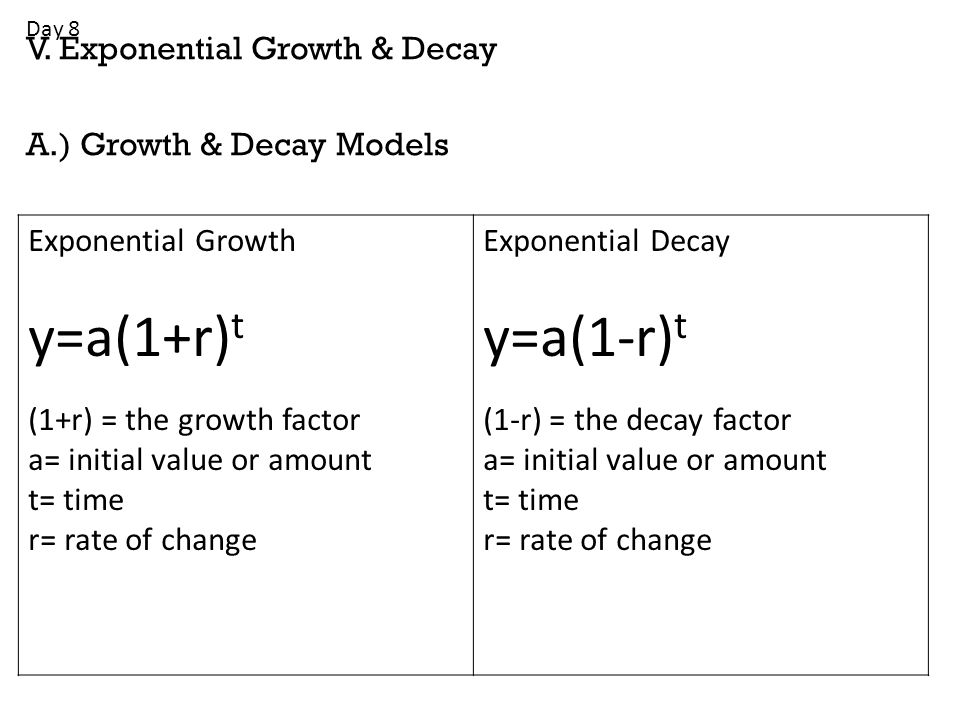
Y=a(1+r)^t 135272-Y=a(1+r)^t
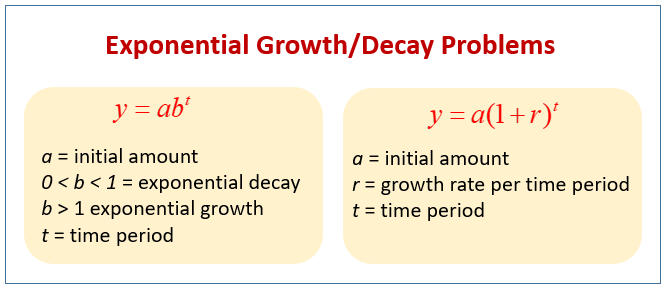
Y = a(1 r)^t Example of Exponential Growth Equation y = 2500(105)^4 Example of Exponential Decay Equation y = 1(085)^6 Exponential Growth Graph Exponential Decay Graph Initial Value (yintercept) "a" in the function y = ab^x Compound Interest Formula A = P(1 r/n)^nt HalfLife Formula A = P(05)^t YOU MIGHT ALSO LIKEThe general equation for depreciation is given by y = a (1 – r)t, where y = current value, a = original cost, r = rate of depreciation, and t = time, in years the original value of a car is $24,000 it depreciates 15% annually what is its value in 4 years?I think you use the following formula y=a(1r)^t where y is the amount after t years, a is the initial amount, r is the annual growth rate, and t is the time in years I will appreciate everyones
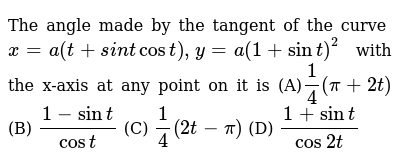
The Angle Made By The Tangent Of The Curve X A T Si N Tcos T Y
Y=a(1+r)^t
Y=a(1+r)^t-Solve for t A=P(1r/n)^(nt) Rewrite the equation as Divide each term by and simplify Tap for more steps Divide each term in by Cancel the common factor of Tap for more steps Cancel the common factor Divide by Take the natural logarithm of both sides of the equation to remove the variable from the exponentExponential decay equation #1 – y = a (1 – r) t y = what's leftover a = what you start with r = rate t = time ex Timmy drank hot chocolate which has 110 milligrams of sugar If the sugar was eliminated from the body at a rate of 12% per hour



R 05 28 09 Hw 73 Pg 477 47 49 50 Pg 490 17 49 61odd Pg 496 31 55 Eoo Pg 505 25 59 Odd 50 V 200 875 T 14 Ppt Download
Remaining grams a = 16 Starting value r = 50% = 05 Decimal form b = 1 05 Decay Factor x = 500 5730 No of Half livesOf the polynomial are r = −1 and −4 The general solution is then y = C1 e −t C 2 e −4t Suppose there are initial conditions y(0) = 1, y′(0) = −7 A unique particular solution can be found by solving for C1 and C2 using the initial conditions First we need to calculate y′ = −C1 e −t − 4 C 2 e −4 t, then apply theThe general equation for depreciation is given by {eq}\displaystyle{ y = A(1 r)t }{/eq}, where y = current value, A = original cost, r = rate of depreciation, and t = time, in years A car was
Answer 3 📌📌📌 question Rewrite the function in the form y=a(1r)^t of y=a(1r)^t Then state the growth of or decay rate Y=a(8)^t/2 the answers to estudyassistantcomAn equation for the depreciation of a car is given by y = A(1 – r)t, where y = current value of the car, A = original cost, r = rate of depreciation, and t = time, in years The current value of a car is $12,250 The car originally cost $,000 and depreciates at a rate of 15% per year How old is the car?Hence, r = 1 = , or, rounding the value of "r" to the nearest tenthousandth, r = 0630 Therefore, your answer is y = 5*()^t It is EXACTLY the form you requested, with the value of r = 0630, rounded as it is assigned by the problem
Rewrite y=(14)^t8 in the form y=a(1r)^t I keep getting the wrong answer not sure if it goes to 4%?Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreAn equation for the depreciation of a car is given by y = A (1 – r)t, where y = current value of the car, A = original cost, r = rate of depreciation, and t = time, in years The value of a car is half what it originally cost The rate of depreciation is 10% Approximately how old is the car?


10 Parametric Equations 26 Polar Coordinates


If Y A Sin Wt Kx Then The Value Of Dy Dx Is A W And T Are Constant 1 A Cos Wt Kx 2 Aw Brainly In
The general equation for depreciation is given by y = A(1 r)t, where y = current value, A = original cost, r = rate of depreciation, and t = time, in years The original value of a car is $24,000 It depreciates 15% annually What is its value in 4 years?Other time period) The amount y of such a quantity after t years can be modeled by one of these equations Exponential Growth Model Exponential Decay Model y = a(1 r)t y = a(1 − r)t Note that a is the initial amount and r is the percent increase or decrease written as a decimal The quantity 1 r is the growth factor, and 1 − r is theX(t) = x 0 × (1 r) t x(t) is the value at time t x 0 is the initial value at time t=0 r is the growth rate when r>0 or decay rate when r


Q Tbn And9gcqijosvjs X3b0gges Uh2g7tqf4q8ek Jt2uxlutl7txidqktm Usqp Cau



Families Of Curves Differential Equation Examples Pdf Familyscopes
👍 Correct answer to the question The general equation for depreciation is given by y = a(1 – r)t, where y = current value, a = original cost, r = rate of depreciation, and t = time, in years the original value of a car is $24,000 it deprecia eeduanswerscom(1 r ) is the growth factor, r is the growth rate The percent of increase is 100 r y = C (1 r ) t 21 E XPONENTIAL D ECAY M ODEL C is the initial amount t is the time period (1 – r ) is the decay factor, r is the decay rate The percent of decrease is 100 r y = C (1 – r ) tQuestion An equation for the depreciation of a car is given by y = A(1 – r)t , where y = current value of the car, A = original cost, r = rate of depreciation, and t = time, in years The value of a car is half what it originally cost The rate of depreciation is 10% Approximately how old is the car?
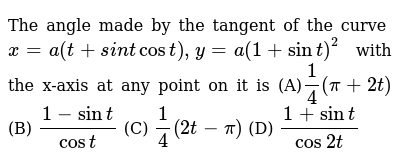


The Angle Made By The Tangent Of The Curve X A T Si N Tcos T Y


Www Wsfcs K12 Nc Us Cms Lib Nc Centricity Domain 1499 Growth and decay student notes Pdf
Solve for t A=P(1r/n)^(nt) Rewrite the equation as Divide each term by and simplify Tap for more steps Divide each term in by Cancel the common factor of Tap for more steps Cancel the common factor Divide by Take the natural logarithm of both sides of the equation to remove the variable from the exponentX(t) = x 0 × (1 r) t x(t) is the value at time t x 0 is the initial value at time t=0 r is the growth rate when r>0 or decay rate when rWarmup y = a(1r)t 10) 00(1 003)1 = $60 11) 0(1 003)10 = $ 12) 600(1 007)4 =$ 13) 1500(1 004)8 = $5285


X 2at 1 T2 Y 2bt 1 T2 Sarthaks Econnect Largest Online Education Community



Exponential Vs Linear Functions Flashcards Quizlet
Rewrite y=a (2)^1/3 in the form y=a (1r)^t or y=a (1r)^t then state the growth or decay rate Mathematics, 0500 NewKidnewlessonsThe decay factor is b = 1 r In this situation x is the number of halflives If one halflife is 5730 years then the number of halflives after 500 years is x = 500 5730 y = ?Using the growth formula we have y = a(1 r) x where a = 1 (we start with 1 bacteria), and r = 100%, since the amount doubles y = 1(1 100) x = 2 x (same result) Notice that the graph is a scatter plot You cannot have a fractional part of a bacteria The dotted line is the exponential function which contains the scatter plots (the model)



Chapter 7 Flashcards Quizlet



The Regression Equation Introduction To Statistics
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history👍 Correct answer to the question Rewrite the function in the form y=a(1r)^t of y=a(1r)^t Then state the growth of or decay rate Y=a(8)^t/2 eeduanswerscomThe figure above is an example of exponential decay In fact, it is the graph of the exponential function y = 05 x The general form of an exponential function is y = ab xTherefore, when y = 05 x, a = 1 and b = 05 The following table shows some points that you could have used to graph this exponential decay


Q Tbn And9gcsxdkye Uvlepw6jnv1xicstcmr 3dgvf Uhidnrjgbl78xevv Usqp Cau



Fabrication And Evaluation Of Evanescent Wave Absorption Based Polyaniline Cladding Modified Fiber Optic Urea Biosensor Sciencedirect
The decay factor is b = 1 r In this situation x is the number of halflives If one halflife is 5730 years then the number of halflives after 500 years is x = 500 5730 y = ?Correct answers 2 question Use the properties of exponents to rewrite y=3e^06t in the form y=a(1r)^t or y=a(1r)^t round the value or r to the nearest thousandth then find the percent rate of change to the nearest tenth of a percent rewritten function the percent decrease is %P = C (1 r) t Continuous Compound Interest When interest is compounded continually (ie n > ), the compound interest equation takes the form P = C e rt Demonstration of Various Compounding The following table shows the final principal (P), after t = 1 year, of an account initially with C = $, at 6% interest rate, with the given
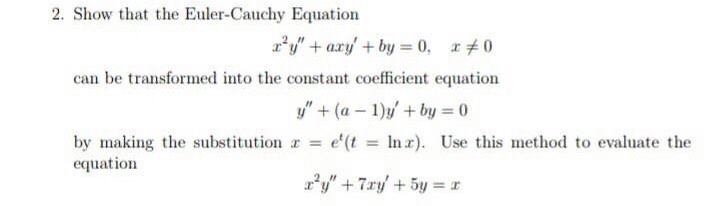


Answered 2 Show That The Euler Cauchy Equation Bartleby



Hardware Implementation Of Hash Functions Springerlink
Growth model y = a(1 r)t must be modifi ed for compound interest problems Finding the Balance in an Account You deposit $9000 in an account that pays 146% annual interestAn equation for the depreciation of a car is given by y = A(1 – r)t , where y = current value of the car, A = original cost, r = rate of depreciation, and t = time, in years The value of a car is half what it originally cost The rate of depreciation is 10% Approximately how old is the car?A)33 years B)50 years C)56 years D)66 years


8 5 And 8 6 Growth And Decay Ch 8 Exponents



Dangers Of Exponential Growth Viruses And Atomic Bombs Fluai
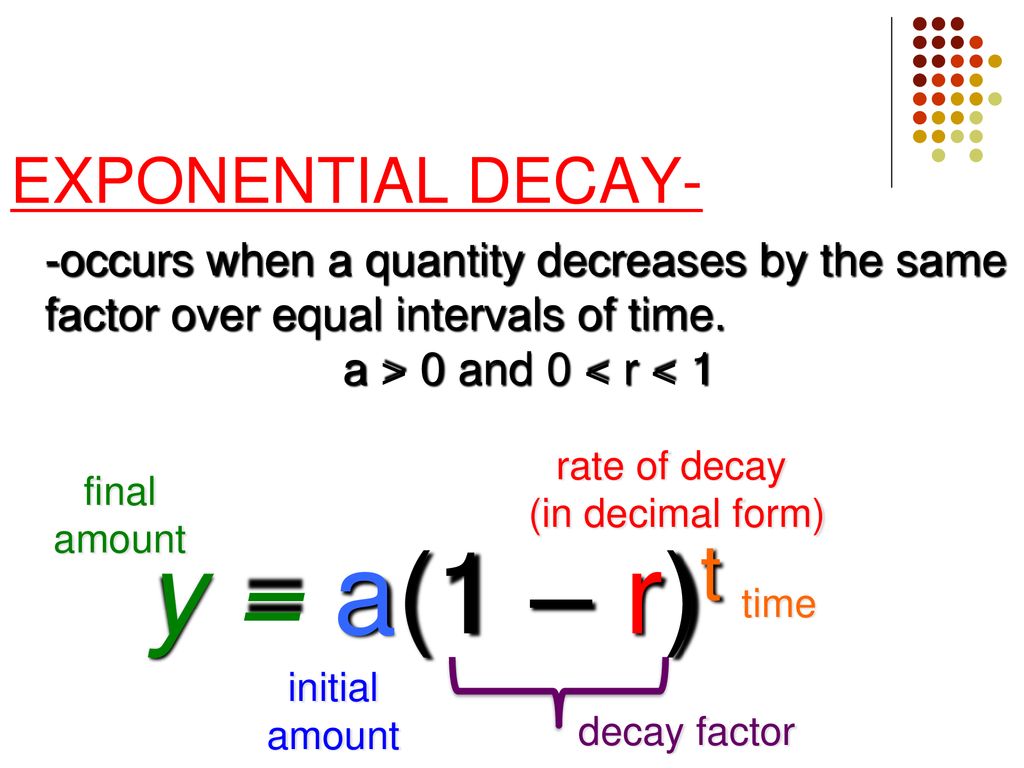
Y = a(1 r)t time growth factor initial amount fi nal amount rate of decay (in decimal form) y = a(1 − r)t time decay factor Practice Check your answers at BigIdeasMathcom Rewrite the function to determine whether it represents exponential growth or exponential decay Then find the percent rate of change 1 y = 80(085)2t 2 y = 67(113)t/4 3 y = 5 ( 3— 2) −8tRemaining grams a = 16 Starting value r = 50% = 05 Decimal form b = 1 05 Decay Factor x = 500 5730 No of Half livesQuadraticFunctionsDay1writtennotebook May 14, 13 Need calculator, graph paper, writing utensil Warmup y = a(1r)t 10) 00(1 003)1 = $60 11) 0(1 003)10 = $ 12) 600(1 007)4 =$ 13) 1500(1 004)8 = $5285


What Do Correlation Coefficients Positive Negative And Zero Mean



Comparing Forms Of Exponential Functions Y Ab X And Y Ae Kx Youtube
Y = a(05) t/x represents the amount y of a substance remaining after t years, where a is the initial amount and x is the length of the halflife (in years) Plutonium238 Halflife years a A scientist is studying a 3gram sample Write a function that represents the amount y ofThe function is of the form y=a(1 r)t, where 1 r> 1, so it represents exponential growth Use the growth factor 1 rto fi nd the rate of growth 1 r= 107 Write an equation Solve for r= 007 r So, the function represents exponential growth and the rate of growth is 7%Answer to An equation for the depreciation of a car is given by y = A(1 r)^{t}, where y = current value of the car, A = original cost, r = rate


Mrsjblanco Weebly Com Uploads 5 3 6 1 Growth And Decay Power Point Pdf



7 1 Exponential Functions Ppt Video Online Download
A L I F I Y A ' S A R T, Mumbai, Maharashtra 239 likes · 1 talking about this Art Logo Design Illustrations Packaging Branding Typography Geometry UI/UX Mural Design CommunicationP = C (1 r) t Continuous Compound Interest When interest is compounded continually (ie n > ), the compound interest equation takes the form P = C e rt Demonstration of Various Compounding The following table shows the final principal (P), after t = 1 year, of an account initially with C = $, at 6% interest rate, with the givenThe general equation for depreciation is given by y = A(1 – r)t, where y = current value, A = original cost, r = rate of depreciation, and t = time, in years A car was purchased 6 years ago for $25,000 If the annual depreciation rate is 11%, which equation can be used to determine the approximate current value of the car?



R 05 28 09 Hw 73 Pg 477 47 49 50 Pg 490 17 49 61odd Pg 496 31 55 Eoo Pg 505 25 59 Odd 50 V 200 875 T 14 Ppt Download



Maths Pages 51 100 Flip Pdf Download Fliphtml5
Y = a(1 r) x Remember that the original exponential formula was y = ab x You will notice that in these new growth and decay functions, the b value (growth factor) has been replaced either by (1 r) or by (1 r) The growth "rate" (r) is determined as b = 1 r The decay "rate" (r) is determined as b = 1 rIdk This equals y = *(14) t By the way the number 4 is 40%2)Find the curvature of r(t) = 9t, t 2, t 3 (9, 1, 1) at the point κ = 3)Use this theorem to find the curvature r(t) = 6t i 4 sin(t) j 4 cos(t) k κ(t) =


2


Www Wappingersschools Org Cms Lib Ny Centricity Domain 848 12 14 6 4 day 1 Pdf
What is the hourly growth rate in the growth formula y=a(1r)^t Answer by nerdybill(7384) (Show Source) You can put this solution on YOUR website!The general equation for depreciation is given by y= A(1−r)t y = A (1 − r) t, where y = current value, A = original cost, r = rate of depreciation, and t = time, in years A car was purchased 6An equation for the depreciation of a car is given by y = A(1 – r)t , where y = current value of the car, A = original cost, r = rate of depreciation, and t = time, in years The value of a car is half what it originally cost The rate of depreciation is 10% Approximately how old is the car?


Do Now 1 22 19 Take Out Hw From Last Week Copy Hw In Your Planner Ppt Download



Ppt 8 8 Exponential Growth Decay Powerpoint Presentation Free Download Id
Suppose y(t) = tr, we have y (t) = rtr−1 and y00(t) = r(r − 1)tr−2 Thus t2y00(t) ty0(t) 9y(t) = (r(r − 1) r 9)tr = (r2 9)tr Thus y = tr is a solution of t2y00(t)αty0(t)βy(t) = 0 if r2 9 = 0 The roots of r2 9 = 0 are 3i and −3i Note that t = elnt and t3i = ei3lnt = cos(3lnt) isin(3lnt) Therefore the generalT y = a(1 r) Exponential Decay Occurs when a quantity _____ by the same rate over time t t = ExamplesExamples 7 The population of a town is decreasing at a rate of 1% per year In 00 there were 1300 people Write an exponential decay function to model this situation Then, find the populationFV = PV(1 i) n R ( (1 i) n 1 ) / i where i = r/m is the interest paid each period and n = m × t is the total number of periods Numerical Example You deposit $100 per month into an account that now contains $5,000 and earns 5% interest per year compounded monthly


The Helen Of Geometry Explore Cycloids Najia Bao Good Morning Everyone Today Let S Investigate And Explore The Helen Of Geometry That Is Cycloid It Was The First Time That I Heard About Cycloid When I Was 12 Years Old My Father A Mechanical



Math 1525 Supplement Sheet For Lab 3
Y = a ( 1 r k) k t, where k is the number of times the interest is compounded per year So, plugging in your information gives y = 3750 ( 1 06 12) 132 = $ Share answered Jan 15 '15 at 129 onetoinfinity onetoinfinity 435 2An equation for the depreciation of a car is given by y = A (1 – r)t, where y = current value of the car, A = original cost, r = rate of depreciation, and t = time, in years The current value of aY = a(1r)t Example 3 Exponential Decay 3a) A fully inflated child's raft for a pool is losing 66% of its air every day The raft originally contained 4500 cubic inches of air Write an equation to represent the loss of air Estimate the amount of air in the raft after 7 days



A New Look At Multi Stage Models Of Cancer Incidence Biorxiv



Calculus 2 Parametric Equations 17 Of Find The Slope Of A Cycloid Youtube
In a labatory, a culture increases from 30 to 195 organisms in 5 hours What is the hourly growth rate in the growth formula y=a(1r)^t y=a(1r)^t The problem gives us y as 195


L Earning T Arget 6d I Can Explain When A Situation Can Be Modeled By Exponential Growth Or Decay Solve The Problem And Interpret My Solution Within Ppt Download


Www Cbsd Org Cms Lib Pa Centricity Domain 1906 Alg2 8 4 exponential growth and decay models pd 1 Pdf


Http Www Cbsd Org Cms Lib Pa Centricity Domain 17 8 1 8 2 exponential growth and decay key Pdf



Hw 5 Sols Pdf Chapter 22 Initial Value Problems Problem 1 Solve The Following Problem Over The Interval From X 0 To 1 Using A Step Size Of 0 25 Course Hero



Essential Skills Solve Problems Involving Exponential Growth Solve Problems Involving Exponential Decay Ppt Download


Prince Bubblegum St 12 Algebra 2 Adventure Time



Chapter 12 Linear Regression And Correlation


4 4 Surface Integrals And The Divergence Theorem Mathematics Libretexts


Www Scarsdaleschools K12 Ny Us Cms Lib5 Ny Centricity Domain 360 Exponentialgrowthdecay Pdf



Ex 9 3 3 Form Differential Equation Y A x B E 2x



Misc 23 If Y Ea Cos 1 X Show 1 X2 D2y Dx2 X Dy Dx



And 3 Find The Eigenvalues And Eigenfunctions For The Given Boundary Value Problem There Are 3 Cases Homeworklib


Http Www Peoriapublicschools Org Cms Lib2 Il Centricity Domain 1464 8th jan 18 Pdf



Compressive Sensing Based Random Access For Machine Type Communications Considering Tradeoff Between Link Performance And Latency Eurasip Journal On Wireless Communications And Networking Full Text



Why Does D Ln Y Dx Go To 1 Y Dy Dx Shouldn T It Be Just 1 Y I Did Not Understand This Passage It May Be Simple But I M Just Begging To Study These Things Thanks A


X Why Exponential Decay


Www Wappingersschools Org Cms Lib Ny Centricity Domain 848 1 3 6 4 day 1 growth and decay Pdf



Rate Of Decay Youtube



Solving Literal Equations Algebra 1 Youtube



Example 33 Find Dy Dx If Y X X Y X X A B Teachoo


Exponential Growth And Decay Examples Solutions Videos Worksheets Activities



The Boundary Value Problem X4 D2y Dx2 Y 0 Y A Chegg Com



Exponential Growth And Interest
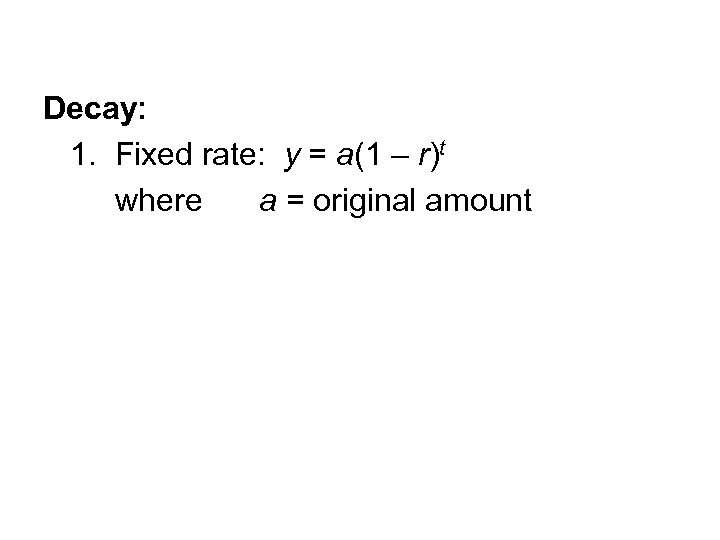


8 8 Exponential Growth Decay


Guarded Cubical Type Theory Springerlink


Http Teachers Sheboygan K12 Wi Us Sdamrow Documents 106pdf Pdf



Solved Consider The Following Equations For Y D And D Y T Chegg Com



Solved Recall That The Arc Length Of A Curve Given By A P Chegg Com



Exponential Growth Decay Ppt Download



Exponential Functions Posters Reference Sheets Bundle Exponential Functions Word Problem Worksheets Exponential Growth



On Fuzzy Normed Linear Space Valued Statistically Convergent Sequences



If X 3at1 T 3 And Y 3at 21 T 3 Then Dydx Is Equal To



Reconstruction Of Bennu Particle Events From Sparse Data Pelgrift Earth And Space Science Wiley Online Library


Http Www Ozark K12 Mo Us Cms Lib011 Mo Centricity Domain 533 Doc Pdf


Www Sccollege Edu Departments Math Documents Math 140 05 04 0 Pdf



Exponential Growth And Decay
.14_4247565755675833184.png)


If X A Cost Log Tan T 2 Y A 1 Sint Find D2y Dx2 Math Differential Equations Meritnation Com



1 Points 18 Consider National Income Model National Income Consumption Investment Government Sector Taxes Y C I G C Homeworklib



You Purchase A Car In 10 For 25 000 The Value Of The Car Decreases By 14 Annually Describe And Correct The Error In Finding The Value Of The Car In 15 Left



Solved Bunter Was Asked To Solve The Following Maximizati Chegg Com
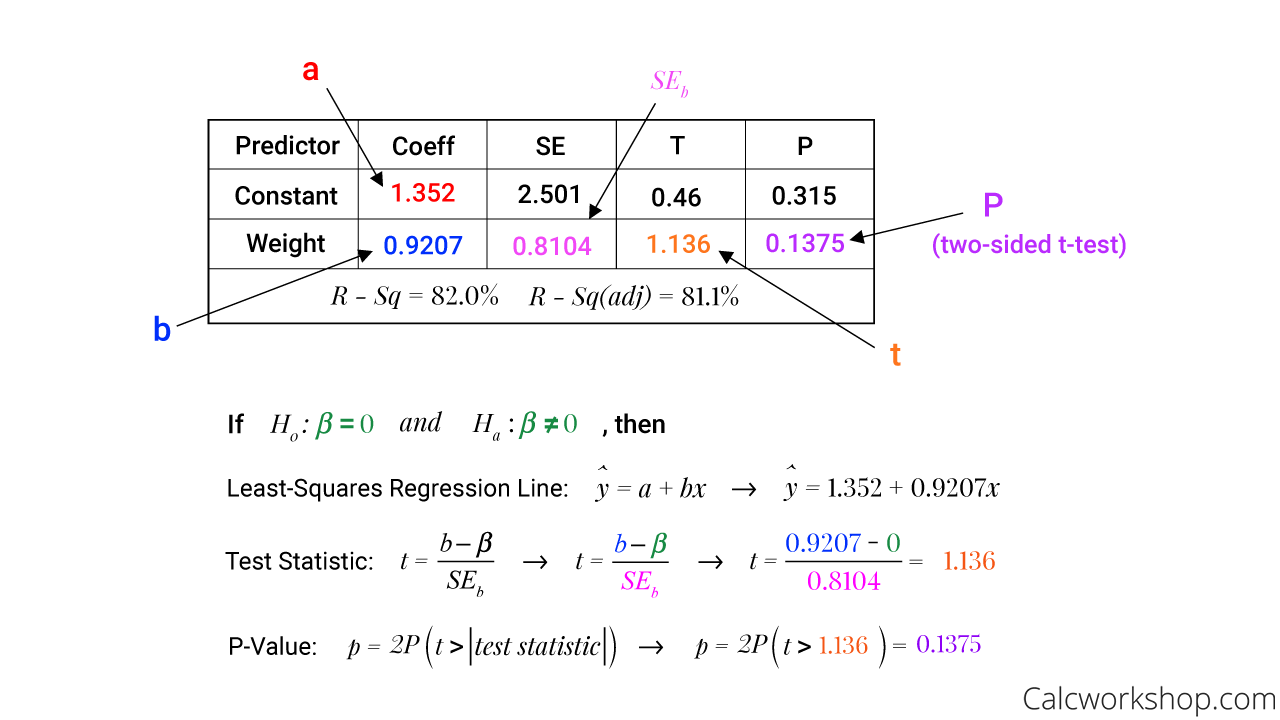


Linear Regression T Test When How W 5 Examples


Q Tbn And9gcqva6kwkjyd2rdsih05tmpg8ppumkliqmlp8mikzy1chqinh1dj Usqp Cau



Ppt Exponential Growth Decay Powerpoint Presentation Free Download Id


Q Tbn And9gcqgxordtnbyapfjd3lmlujrvslb5x3ac Hjy Sjwpnftor78qyt Usqp Cau



Let V Be The Vector Space Y A Betax Alpha B Chegg Com
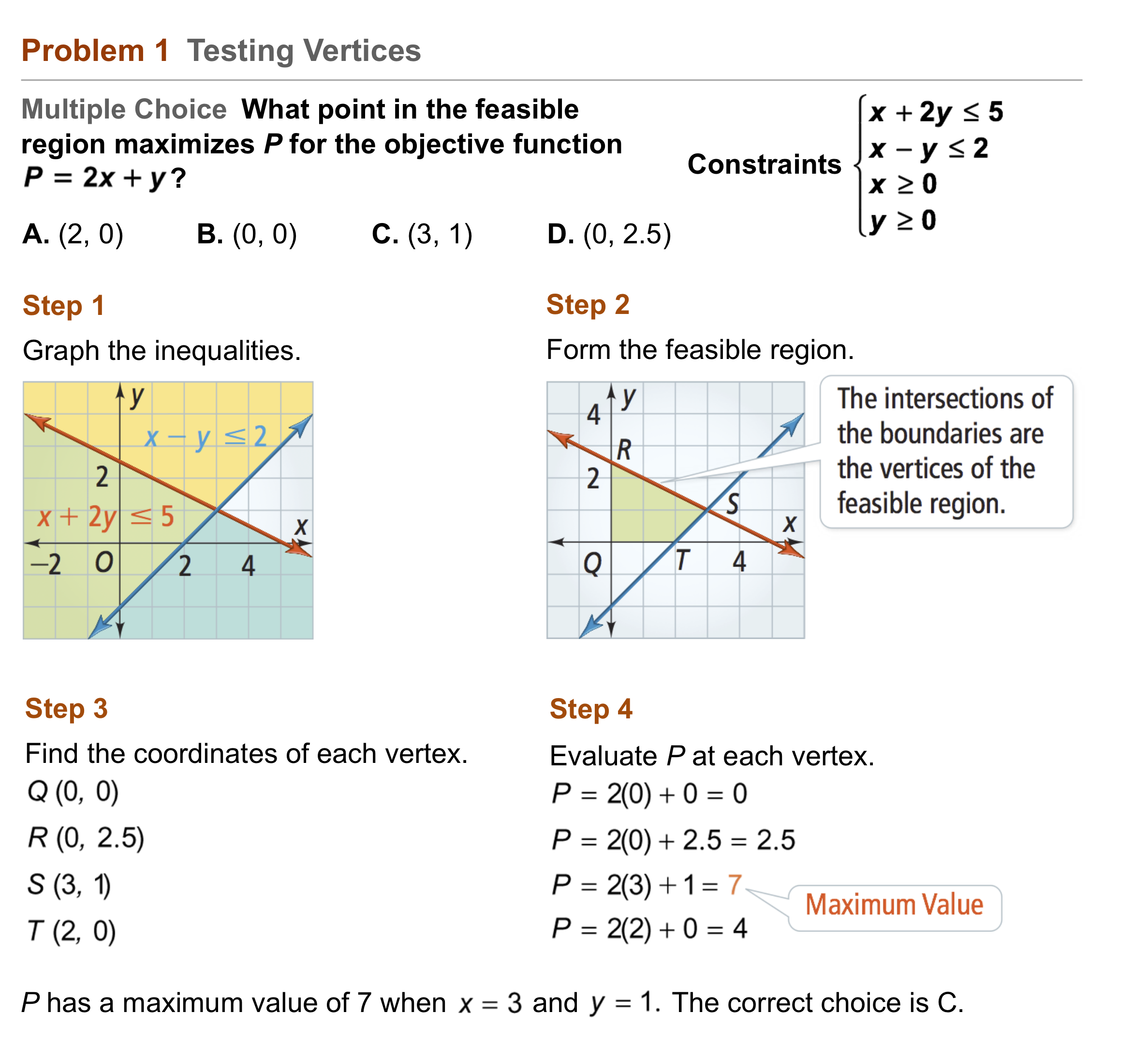


Algebra 2 3 4 Complete Lesson Linear Programming Matthew Richardson Library Formative



Solved 3 12 Thermistor Transfer Function The Transfer Fu Chegg Com



R Markdown Inline Latex Equations Vs Stack Overflow


Www Marsd Org Cms Lib Nj Centricity Domain 8 6 1 6 2 review key Pdf



8 8 Exponential Growth Decay Decay 1 Fixed Rate Ppt Download


Exponential Decay And Growth Home


Http Www Mpsaz Org Rmhs Staff Esritter Algebra2 Files 6 1 6 4 Review Key Pdf



Mechanics Ap Physics C 1995
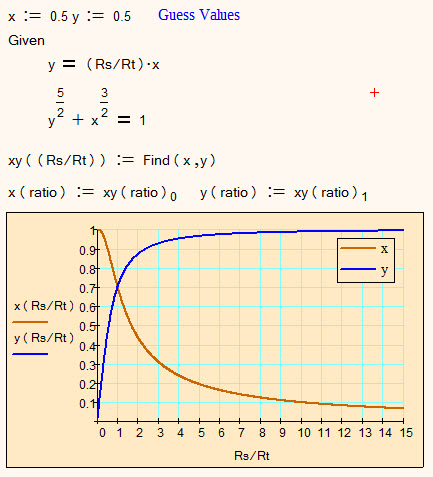


Intercept Of Two Equations Y 2 5 1 X 1 5 And Y Ptc Community



Objectives Understand The Exponential Growth Decay Function Family Graph Exponential Growth Decay Functions Use Exponential Functions To Model Ppt Download


Http Www Mtsd K12 Nj Us Cms Lib5 Nj Centricity Domain 378 4 1 4 2 packet answers Pdf



Openstax Statistics Ch12 Linear Regression And Correlation Top Hat



Exponential Growth And Decay



Misc 16 If Cos Y X Cos A Y Prove Dy Dx Cos2 A Y



Exponential Growth And Decay Flashcards Quizlet


Http Www Manhassetschools Org Cms Lib8 Ny Centricity Domain 710 Hw 80 key 9h Pdf



Exponential Growth And Decay Youtube



Ex 1 A Cup Of Coffee Contains 130 Milligrams Of Caffeine Flipbook By Fliphtml5


Exponential Growth And Decay Posters And Reference Sheets By Plan Teach Math


Www Strongnet Org Cms Lib Oh Centricity Domain 990 9 3 guided notes key Pdf



The Locus Of A Point Reprersented By X A 2 T 1 T Y A 2 T 1 1



Calculus 2 Parametric Equations 18 Of Find The Area Of An Arch Of A Cycloid Youtube



Solved 2 Assume A Closed Smooth Curve Y A B R2 Chegg Com


Eleceeng234 Analytical Methods In Engineering 2nd Order Homogeneous Differential Equations Report Writing Engineering Assignment Help



Exponential Growth And Decay By Shaikha Arif Grade 10 Mrs Fatma Ppt Download



Substituting Numbers Into Formulae Mr Mathematics Com


If X A 8 Sin8 Y A 1 Cos8 Find D 2y Dx 2 Sarthaks Econnect Largest Online Education Community


Intercept Of Two Equations Y 2 5 1 X 1 5 And Y Ptc Community


Using The Ti And Ti 84 Calculators Open Textbooks For Hong Kong


コメント
コメントを投稿